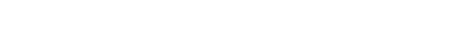SYNTHETIC TOP LAYER FOR A WINTER MUMMY BAG?

[Eric Blumensaadt]

MY BASIC QUILT NEED:

I just want to trap condensation 9mostly as frost) so ‘topper” warmth ain’t a consideration. Both my LL Bean winter -20 F. down mummy and 3 season Western Mountaineering Megalite mummy are large enough to easily accommodate light insulated down clothing or 300 weight heavy fleece.

Bill and “nunatak”, thanks for the info on the AD “as-is”. The Alpha Direct is looking better and better. I would just sew male QR buckle halves to it and use light elastic bands and the other half of the buckles to hold it around my mattress. As long as the sides and top of the mummy are covered I’m good. The winter mummy has DWR treated down so some moisture on the bottom is OK for a week long trip. A Ridge Rest foam mat under an R 5.3 insulated mattress will be fine. I also put outer clothes under everything to keep them from getting frozen stiff. It actually helps insulate.

Thanks to everyone for the help. Who knows, this thread may help others too.

 

[Stephen Seeber]

Warmth is the consideration.  Without sufficient warmth, you cannot move the freeze line far enough out of your bag to matter.  How much warmth you need to yield an improvement is a function of the temperature rating of your existing bag and the temperatures at which you plan on using it.  I am working on an upcoming article that will quantify these issues. You seem to imply that you plan on adding clothing or insulation inside your bag.  I wear some clothing in my bag to increase warmth. However, the impact of adding insulation inside your bag will be to move the point at which vapor freezes in your bag’s insulation closer to you.  If you are going to be in temperatures cold enough to cause freezing vapor in your bag, this is not the strategy to pursue.  Here is an example based on the current version of my calculations:  If I am in my Alpinlite bag at an ambient of 25F, the vapor I produce will freeze at .1″ from the top surface of the bag. In order to raise the temperature enough to move vapor (and the freeze point) completely out of the bag, I need to add a topper of 3 ounces per square yard Climashield Apex.  The same job can be accomplished by 3 layers of 4004 AD, which will have a weight of  17 ounces per square yard. If a 17 osy quilt does not deter you, you could try fleece, which will be even heavier. Of course, as the ambient temperature drops further, a heavier topper will be required.  There is no magic bullet here.

[Eric Blumensaadt]

I really don’t need more warmth for either my overstuffed WM Megalite (+20 F.) or my LL Bean -20 F. down bag. All I want is a condensation trap. Maybe if the AD material dries faster and is more compact that is my best bet. I have been Climashield fan ever since the’90s when a PrimaLoft mummy lost 80% of its loft after just ONE summer use and being properly stored loosely in a huge cloth storage bag, hanging vertically.

[Kevin O]

I am by no means an expert on high efficiency wall construction. In my research for some home repairs I came across the following that I think offers information about where the dew point is located in an insulation system. If anyone is more knowledgeable or sees a flaw about this I am more than happy to be corrected.

This is a diagram and a chart from a guide on building wall assemblies to deal with cold weather condensation.

Hypothesizing that this an effective representation of a dual quilt system (down as the the inside wall insulation and synthetic as the blue insulation). The premise is that you want to push the dew point outside the condensation absorbing inner batt insulation and into the water impervious outer foam insulation. This is done by placing a layer of sufficient r value and air tight rigid foam insulation  exterior to the batt insulation to keep the inside wall cavity above the dew point.

If we suppose the mechanism here is the same we can see that the image shows how the temperature change across layers of insulation results in the location of the dew point. The ratio of inner and outer insulation r value determines the location of the dew point and this chart shows the minimum ratio to keep the dew point out of the inner insulation for a given rh and temperature.

Table 1: Ratio of exterior-interior insulation to control air leakage condensation

This becomes problematic for our current overbag strategy. As relative humidity increases you need more and more external insulation to maintain the location of the dew point.  A quilt system with >50% of its total insulation as a second synthetic layer is well beyond the standard 50* synthetic. If we have bags with reliable temperature testing (e.g. a 20* down bag is equivalent to a 20* rated synthetic bag) we would actually need a  synthetic overbag that is rated to be equal or warmer than the inner down bag if our goal is to maintain the dew point in the synthetic layer.

TLDR: for an interior rh and exterior temperature we are likely to see while backpacking you are likely to need your synthetic bag to be a significant percentage of the total sleep system insulation in order to keep the dew point out of the inner bag and enabling the synthetic insulation to catch any condensation.

The above information comes from here: https://buildingscience.com/documents/digests/bsd-controlling-cold-weather-condensation-using-insulation

[Stephen Seeber]

Kevin, you are correct. I have done the calculations and they are consistent with your posting. Eventually, I will produce an article on this, but I do not believe low R-value top quilts can move the dew point or freeze point far enough to do any good.  As you point out, R-values that might get the job done are impractical.

[Kevin O]

Stephen,

I am happy to hear my random musings have some basis in reality. In my experience of short trips where condensation is less of a concern I’ve found lightweight over bags to be useful to manage moisture from tent condensation. I wonder about the use of a vapor barrier inner layer if preventing condensation build up is a priority.
I am curious to see what the weight and size look like for a dual system with a lighter inner down bag and an appropriate sized synthetic overbag vs just using a synthetic bag.

 

[Alan W]

Stephen and others seeking to “calculate”, be careful with assumption blind spots; but don’t let the following prevent efforts.

If we were only interested in where freezing temperature of 32F is reached, just the insulation R values are sufficient. E.g., as in the house construction example above where an impermeable membrane is postulated.

However, I suggest we are after pushing the condensation point into the top layer, content to let it freeze there.

AND in our sleeping kit system, we do not have an impermiable membrane reducing the system to heat transfer only.

In our sleeping kit, condensation involves both heat transfer and MASS transfer.

Very importantly the MASS transfer involves migration of very dry (cold) outside air inwards as well as migration of water vapor outwards.

How restless is the sleeper?  How tight is the seal between layers? How windy the location?

And system pressure (altitude) matters also for the dew temperature.

The variables are sufficiently numerous and interactive that field experience (reality) may be needed to calibrate backwards the MASS transfer issues of cold dry air moving inwards as well as moisture transfer outwards.

Bulk flow of mass, eddy diffusion of mass, and molecular diffusion of mass are all factors in a sleep kit.

Again, be intentional and explicit with assumptions needed to calculate.

[Kevin O]

By no means do I wish to portray a complete representation of the dynamics of a sleep system in using housing construction as a model, but I believe this model provides more information than the assumptions that putting any synthetic layer on top will  be sufficient.

To your point about impermeable layers, the point of this wall assembly is to not have an impermeable layer, the rigid foam insulation although air tight does allow moisture transfer through vapor, enabling drying from the inside out. There is no vapor barrier installed in this method.

[Alan W]

Kevin, your note of Mar 20th stated “– into the water impervious outer foam insulation”.  The foam is defined as an impermeable membrane with respect to water.

However, I take your point the layer could be a gas-permeable membrane, just as our sleeping quilts are gas-permeable.

My point was that our sleeping quilts and bags ARE gas-permeable and that an analysis of only temperature profile is insufficient to determine their wetting/freezing profile.

Let’s reflect that clouds do not form and that rain, sleet, hail, and snow do not necessarily occur whenever the local atmospheric temperature is at/below 32°F.  E.g., it can be 0°F with crystal clear skies.

Besides temperature, the local pressure (mainly altitude) and the local mole fraction of water vapor interact with the local temperature to determine whether there is water condensation and/or deposition, which is the reverse of sublimation and forms frost & snow.  (Snow forms without water droplets; water droplets equal rain, sleet, hail).

Temperature alone is an insufficient factor, an insufficient analysis, to determine the presence or absence of clouds, snow, rain, etc.

The same is true in our sleeping kit.  Temperature profile is informative, but it is not definitive for condensation or icing without reckoning the water vapor profile.

Importantly, the same thing that dominates the loss of heat, namely the macro, meso, and micro motion of gas molecules, is also moving water molecules from higher concentration at the inside of the quilt, through the quilt, and completely out of the quilt.

Both heat (BTUs, etc.) and water vapor have an outward flux through the quilt and into the surrounding air.

The amount of heat that our bodies generate matters.

The amount of water vapor that our bodies and possibly wet clothes generate matters.

The resistance to heat loss and to water vapor loss completely out of the quilt do not have to be equal magnitude; but they are both significant in magnitude.

Temperature profile alone is an insufficient factor, an insufficient analysis.

As best I presently appreciate.

[Stephen Seeber]

Hi Alan:

I have read your postings with interest and considered their relevance to the questions I am seeking to answer.  I am seeking to answer this question: how much additional insulation is necessary to move the temperature at which condensed vapor freezes outside of a sleeping bag?  I am assuming that condensation and freezing do occur.  I am not concerned about how much vapor is condensing and/or freezing at this stage.

I am taking this approach because, so far, I have not developed methods to determine how much vapor the sleeping bag occupant produces, what the vapor concentration profile across the bag is, and, therefore, where condensation may occur. These are the questions I think you are asking. They are worthwhile questions, and perhaps, ones you already have figured out how to answer.

As part of another project I am working on, after each night of sleeping in my tent in cold weather, I have weighed my sleeping bag and top quilt (when used) to determine how much moisture is trapped.  I have acquired thermal images to identify the location of the trapped moisture.  Under the various conditions I am exposed to, I know that condensation occurs, how much condensation is trapped, and approximately where it is located.  I can also get a sense of how effective the top quilt may be.

Here is an IR image of a top quilt that contains 1.95 ounces of moisture:

 

I am fairly confident I can answer the question of how much extra insulation is required in a top quilt to prevent vapor from freezing in a sleeping bag. However, as you suggest in your posts, the question of how to prevent vapor from condensing and accumulating in a sleeping bag is more complex. If you have techniques to answer this question, I would be happy to learn of them and, if you’d like, work together to see if adding extra insulation outside a sleeping bag is a solution.

Please feel free to respond here, or, send me a PM.

[Alan W]

Stephen, great picture and actual weight!   Thanks.  Hmm, the mass of ice is far less that typical insensible perspiration per 6 hours.  Hmm, why is the ice in the center axially, rather than the edges?  Data is teaching something here.  I look forward to your article with more data and your analysis.

In principle, we know how to do engineering estimations of mass transfer flux and water vapor concentration profile.  As you observe, what we perhaps lack (or do not recognize) is mass transfer data for our typical sleeping kits — AND acceptance that a very great number of simplifying assumptions are needed to do practicable calculations of even the thermal profile.

Probably you already know that the engineering models (equations) for MASS transfer are directly analogous to heat transfer models.

For uniform 1- dimensional planar mass transfer flux through a uniform resistance, the transfer rate = (driving force)/(resistance), which is the same engineering model (approximation) used for thermal transfer.

o   For heat transfer the driving force = Temperature difference = dT

o   For MASS transfer the driving force = Concentration difference = dC, at least for chemically simple systems, and water vapor in air qualifies.

o   Of course, our sleep kits are not actually uniform, planar 1-dimensional systems.

Importantly, the Resistance value for MASS transfer is not numerically the same as the resistance value for heat transfer regardless of any reasonable choice of units.

Although resistance to thermal and mass transfer through our sleeping kit both relate principally to macro, meso and micro movements of air (gas) molecules, the two resistances are only loosely coupled.  Their ratio will be affected by very many details in the quilt constructions, as well as the numerical unit systems chosen.

For an extreme example, consider a down quilt which will perforce have a tightly woven, probably calendared down-proof fabric, maybe thinner, maybe thicker, perhaps with DWR or even waterproof-breathable Pertex; and consider another (outer) quilt that is made with layers of Alpha direct covered by no-see-um netting, trusting the tent to kill all wind and the no-see-um to prevent snagging.  The two quilt constructs will have much different empirical resistance ratios for Rthermal to Rmass.

Rigorously, the equations (models) for heat and mass transfer are differential and require calculus to solve.

Rigorously, the local values of T can affect the local values of both Rthermal and Rmass; and similarly, the local values of C can also affect the local values of both Rthermal and Rmass.  Certainly, this occurs where water condensation or ice deposition occur.

Often a significant number of simplifying assumptions are “close enough” and “good enough” to reduce the solution to relatively simple algebraic forms, especially in 1-dimensional systems; BUT proceed very cautiously to avoid a facile, glib oversight.

For estimating dew temperature, deposition temperature (frosting) and concentration of water vapor in air at sea level at different relative humidity percentages as a function of temperature, consider equations in following article:

Huang, Jianhua, “A Simple Accurate Formula for Calculating Saturation Vapor Pressure of Water and Ice”, Journal of Applied Meteorology and Climatology, Volume 57, pp 1265‐1272, DOI: 10.1175/JAMC‐D‐17‐0334.1

———————

A  little CV:  I did chemical engineering graduate research in mass transfer at Univ of Texas in the 1970’s.   Retirement from full time work was in 2012, and active consulting continues.  In Q4-23, I provided an unsteady state counter-current diffusive mass transfer model with thermal variables. The Excel model file size was over 11 MB; and an 8-figure capital project is now resulting.  I’ve directed unsteady state 3D, 3-phase (solid-liquid-gas) models of coupled mass, momentum and heat transfer using commercially available Computational Fluid Dynamics codes.  Running on multiple PCs in parallel each with 4 to 8 high speed cores, the CFD models take calendar weeks to reach pseudo-steady-state chaos, providing TB-sized output data files, further compressed by statistical analysis in Excel to MB sizes for graphical display and analysis.  I am an inventor on over 75 US patents to date.

There is more that I don’t know about heat and mass transfer than what I do know.

I tend to make things too complex before simplifying; and I’m likely still in the too complex phase when considering our sleeping kit from an engineering view.

Although I recognize that both heat transfer and mass transfer affect when (if) and where condensation and deposition may occur in our quilt systems, I thus far suspect that heat transfer aspect is more important based on anecdotal evidence.

However, the condensation and icing events are actually due to mass transfer ills, viewed as either too much water vapor moving into the insulating layers or too little water vapor moving all the way through the layers.  Thus, we neglect mass transfer at peril until we have modeling or experience to validate our relying principally or only on temperature profile.

As I seek to reconcile modeling with anecdotal experience, mainly others, I’ve gotten far enough to believe the system is so complex and variable (kit, individual, weather) that modeling will only provide general guidance for layering, say a 10°F range of ambient for a given thermal resistance ratio of quilt layers.  (may follow with another post of assumptions and calculations)

I often camp multiday below 32°F down into the teens, but only very rarely below 10°F.  I use single layer quilt or bag. Depending on location, season and hike length, I use foam or inflatable mattress, or both.  My icing experience is very little (thankfully) with my coldest nights having been quite dry and windy ambient with me also cool and dry at bedtime.  I’ve hiked all of the AT, CT, Ouachita Trail; parts of AZ trail, CDT, PCT; Denali; 46 ascents of CO 14ers; and I typically do 2 to 5 weeks per year of Wilderness Area volunteering, mainly crosscut & axe trail clearing (CO, NM, AR, MN, AZ, TN).

[Stephen Seeber]

Hi Alan:

I enjoyed reading your thoughts on the subject. The article you suggested is readily available as a PDF, so I now have it. I agree with you that existing discussions on this subject seem anecdotal. Based on the calculations that I have already made, I am skeptical that the over-quilt approach will be effective unless substantial insulation is added.

Concerning the image.  No wetting on the edges because those are tucked beneath my pad. No ice.  Just liquid water. As you can imagine, the moisture’s location simply corresponds to my body’s location. Most of the water is condensed on the fabric.  Without putting a hole in the fabric, I cannot confirm, but I don’t expect much water to be contained in the insulation.

I will try to send you a PM today or tomorrow to discuss alternate approaches to studying this issue.

[Jerry Adams]

“I often camp multiday below 32°F down into the teens, but only very rarely below 10°F.”

I don’t go much below 20F – no icing

Anecdotally, this is a problem at temperature less than 10F.  And multiple days.  As described by Stephenson.

[Alan W]

Gerry, thanks for the Stephenson reference.  I’m only faintly aware of his artic struggles and did not know he settled on a 10°F ambient bogey for icing woes.

The closest I’ve come to ice troubles was 4 consecutive nights bivy camped atop light snow cover on North Rim GCNP with temperature in the teens in Feb-22.  Then, a multiday descent down the Nankoweap Trail cured the loss of loft.

I’ve puzzled over the focus on temperature profile in quilts for what is actually a mass transfer issue.

Surely the amount of water vapor formed inside the sleeping kit (cool dry hiker at bedtime vs. overheated hiker with lots of wet clothes to dry) also matters.

Surely the ambient humidity matters, for more ambient humidity reduces the rate at which water vapor leaves the sleep kit.

Also, the relative resistance of the quilt(s) to water vapor mass transport is only loosely linked to the resistance to heat (enthalpy) transport.

—  The ratio of the two transport resistances can be different for different constructs, which is what Stephen has been studying for torso clothing in recent months.

—  For sleeping kit, an extreme example of divergent resistances is absolutely no water transport when using a VBL, but heat transport continues.  (If only it were easy to pull off the reverse “trick”.)

Furthermore, the water vapor loss out of the quilt system is not negligible, even after icing onset; but it is insufficient to prevent further icing.

————–

Finally, maybe, the underlying reason is finally dawning on me for why the mass transfer problem (condensation and/or icing from too little water vapor leaving the quilt) is usefully viewed as mostly a thermal problem.

Many may go ‘duh’ for this; but different folk assimilate information differently, and I can be a bit tangential and sometimes slow.

The reason is likely that local temperature also dominates the vapor pressure of water, and thus local temperature dominates the local transport rate of water vapor.

Too little amount of water vapor transport rate, relative to vapor formation rate from our bodies (and wet clothes), leads to either condensation (“dew”) or deposition (frost”) inside our sleep kit, and both are bad for loft and thermal transport.

EVENTUALLY at steady state (my thinking was stuck in unsteady state start up sequence), the lowest temperatures in the sleeping kit dominate the GLOBAL STEADY STATE loss rate of water vapor completely out of the sleeping kit.

Unfortunately, it seems that even without piling lots of wet clothes inside, our bodies continuously pump out more vapor than can be transported by the saturation vapor pressure of water occurring when local quilt temperature drops too cold, somewhere in the region of “freezing”.

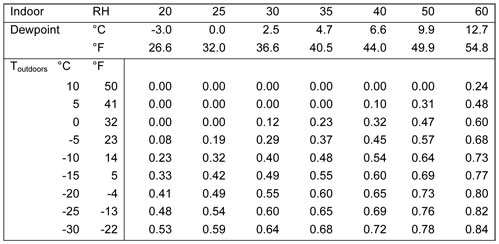
This is because the saturation vapor pressure of water rapidly (about exponentially) declines and becomes a very small value with colder temperatures.  Even after ice is formed, the vapor pressure of ice is still strongly reduced by ever colder temperature.  Tables of water vapor saturation pressure data are attached, taken from the Huang reference.

When temperatures drop below 40, then 30, then 20, then 10°F, ramping up the quilt thickness for more thermal insulation (about linearly) is working directly against the need for less resistance against mass transport due to the super-linearly declining saturation vapor pressure of water.

It’s perhaps obvious in retrospect.  Apologies for slowness to recognize.

Condensation of liquid water can also severely hurt the loft and insulation of down, eventually leading to icing even if not starting with icing.

Thus, 32°F may not be a singular, magic number for the boundary temperature between 2 quilts; but it is certainly in the range where we are rapidly losing digits and adding decimals in the saturation vapor pressure of water.

This recognition may not lead anywhere new and different, or it might.  (And, I do not purport to be the 1st to appreciate this aspect.)

[Alan W]

Now, let’s focus solely on a thermal profile, parking issues relating to the water vapor profile and water vapor transport rate.

 

All models are wrong; and some models are useful.  (Not original.)

Thus, carefully list and respect the limitations for any model.

 

Following is a recitation of assumptions (simplifications) needed to build a simple, perhaps good enough, algebraic thermal model of our sleeping kit (sleeping quilts and bags, possibly layered; hereafter just sleeping kit for brevity) seeking to force icing into an outer, non-down layer.

First, we can have water condensation and ice deposition with our sleep kit WITHOUT being below 32°F ambient, with or without a person inside, with or without a Vapor Barrier Liner (VBL).  We call these events dew and frost, and they occur due to radiation cooling into deep space when the ambient humidity is great enough.  Thus, let’s assume usage of a covering tent or tarp to eliminate radiation cooling.  This matters significantly for the outer surface temperature of the kit.

Next, our sleeping kits are NOT solid, isotropic thermal barriers with uniform thickness.  They are not like a solid piece of metal or polymer.  They do not have true-solid-phase resistance (or conductivity) for heat (or mass) transfer, and they are not uniform in thickness.

The true physical reality of our sleeping kits is a complex, non-isotropic structure of varying thickness.  Sure, we often use the simplifying modeling and calculation concept of equivalent, lumped-effect R-value resistance, as if the insulation were a solid, isotropic material; but this is not reality.

Our sleeping kits provide insulation principally by restricting the macro, meso and even micro scale circulation of air, but down plumes and synthetic batting do not fully eliminate these movements of gas molecules.

(For deeper appreciation, reflect on goose down plumes vs. eider down plumes of equal loft rating; vacuum thermos-bottle type insulation; closed cell foam vs. open celled foam; a sleeping kit made of 3- or 4-inch-thick aerogel;  Alpha direct insulation vs. Apex at the same thickness; etc.)

 

With that understanding, what else can disturb/augment gas molecule motion inside the sleep kit?

·       External wind if strong enough can penetrate some fabric layers (and it can even move the shape of the kit causing “breathing” around the neck, for example.)

·       A person breathing (thorax expansion and contraction) and especially a person tossing and turning continuously change the natural air movements inside the insulating layers.

Thus, let’s add 2 more simplifying assumptions: de minimis wind and a static human.

 

Let’s assume planar geometry.

·       Cylindrical coordinates are closer to truth, though still not reality; but cylindrical coordinates cause messy calculus – and messy algebra after other assumptions.

·       A planar assumption is not self-evidently apt without further understanding; for, seemingly strangely, adding ever thicker insulation on cylindrical piping can lead to more heat loss instead of less.

·       However, for the dimensions of a human body and for a typical sleeping kit with de minimis wind, analyses not covered herein recommend that planar coordinates are a useful modeling simplification.

Assuming planar geometry also implies negation of the head and foot zones of the sleep kit.  Of course, we know this is not true.  The head zone can be particularly important for a quilt without a draft collar.  All such air-leakage zones (and entrance zones) are particularly important to the total heat loss and the temperature (profile) inside the sleep kit.  (Moreover, an AMPLIFIED ditto applies for the mass leakage of water vapor since the water vapor content near the body is non-linearly greater than in outer layers of the sleeping kit.)

Assuming planar geometry also means assuming a uniform thickness of the sleeping kit, or else we are back into multidimensional modeling.  Of course, thickness is not at all uniform: sewing and baffles are real, maldistribution and thin spots are real, and these flaws have disproportionate heat loss (and water mass loss).  This is essentially a repetition of issues for the head and foot zones; but it applies to the entire surface of the kit.

Assume uniform temperature on the inside surface of the sleeping kit.  Of course, we know that this is not true: feet get cold, body & clothing touch sleeping kit in some places but not others, etc.

Assume a uniform temperature on the outside surface of the sleeping kit.  Of course, air currents and boundary layer resistance to heat (and mass) transfer are variable over the surface of a sleeping kit, even without any wind, because of natural convection due to the pseudo-cylindrical shape.

Assume completely uniform lumped-effect thermal resistance of the sleeping kit, with insulation and fabric combined into a single effective lumped-effect average value.

If more than 1 layer is used, make some sort of assumption about the contact and air currents where the 2 quilts interface.  Furthermore, assume that this thermal linkage is invariant over the adjacent surfaces of the 2 layers.  Of course, we know the 2 quilts are not bonded together and that they do not have uniform connectivity over their respective adjacent surfaces.

For simplicity, assume that there is not any added thermal resistance at the boundary of the two layers.  (Optionally, since there actually is added resistance from any air pockets at the boundary between layers, one can add a bit of thermal resistance for the boundary by including it with the resistance of either the outer or inner layer.)

Assume the sleep event is long enough to reach a steady state thermal profile.

Assume that the heat capacity of air is about constant, so that usage of a single average value causes the term to cancel out from the energy balance ratio used hereinafter.

(We do not need to make any assumption about elevation (system pressure) because we are not dealing with the mass transport of water vapor; we are just considering thermal profile.)

 

Whew!  With all these modeling assumptions, and perhaps more overlooked, there are relatively simple algebraic formulae for thermal profiles in multilayer insulating systems.  These have already been recited by others within BPL, but they are now repeated.

Quilt 1 (inner) has uniform, lumped-effect average resistance of R1.

Quilt 2 (outer) has uniform, lumped-effect average resistance of R2.

 

Quilt 1 has an actual uniform inner surface temperature of T1.

Quilt 2 has an actual uniform outer surface temperature of T2.

 

The temperature Tb (temperature at the boundary between the 2 layers) is modeled as follows:

(T1-Tb) / (Tb-T2) = R1/R2

(T1-Tb) = (Tb-T2) * R1/R2

 

Usefully, the units of R1 and R2 cancel out.

For example, we can explore a case where R1 ~ 6 (ft2-°F)/(BTU/hr) and R2 ~ 2 (ft2-°F)/(BTU/hr), or 7 and 2.5, or whatever – if we have useful estimates of the respective R-values.

Optionally, if we can estimate that the (thermal resistance of insulation per unit thickness in Quilt2) = k * (thermal resistance of insulation per unit thickness in Quilt1), then we can compare the ratio of R1/R2 based on the thickness of each layer without even knowing actual R values.

E.g., R1/R2 = (thickness layer 1)/(k *thickness layer 2), with k an empirical value.

 

Next, we come to the thorny issue of the actual values to plug in for the inner (T1) and outer (T2) temperatures.  Even though we have already assumed that each is invariant over its respective planar surface, we have yet to grapple with the actual values of T1 and T2.

The inner temperature is particularly fraught.  Is the person naked or wearing clothes, and how many layers of clothes?  If a person is an ultralight hiker wearing most of their carried clothing to bed, including down parka and down pants, we are dealing with at least a 3-layer system.  Sure, the above algebra extends to 3 layers; but this extension comprises yet another set of simplifying assumptions, and we will still be faced with needing to estimate a uniform temperature over the inner surface of Quilt1.

To cut through the issue of insulation from worn clothing, let’s postulate a consideration for when T1 is about 92°F.  Conveniently, 92-32 = 60°F dT from inner to freezing at atmospheric pressure.  (Chose a different value for T1 if you wish, and proceed accordingly.)

 

Next, let’s say that we want to know what value of outside temperature produces a value of Tb that is exactly 32°F.  The algebra for the model with all the above simplifying and focusing assumptions becomes:

T2 = 32 – (92-32)* R2/R1 = 32 – 60*(R2/R1)

The following table shows different ratios of ever thicker layer 2, i.e., ever greater R2 compared to R1.  If inner and outer layers have the same thermal efficiency per unit thickness, the values can also be viewed as thickness ratios.

R2/R1   T2 (when T1 = 92 °F, Tb = 32°F)

1/5        20 °F

1/4        17 °F

1/3        12 °F

1/2.5       8 °F

1/2          2 °F

1/1.5      -8 °F

1/1        -28°F

 

However, in the real world: winds do change the actual surface temperature T2;  worn clothing does change actual inner temperature T1; variations in thickness of layers and in how they touch do occur; etc. for all the other simplifying assumptions.   I expect at least ±5°F variation in actual field (anecdotal) results compared to the above table.

 

Still, it’s a useful guide (as others found long before me).

·       If we want to force icing into the outer layer only, the inner layer cannot be too thick relative to the outer (e.g., cannot use a 5” down layer with a 1” Apex outer layer at 0°F)

·       The colder the ambient that we wish to endure, the thicker and thicker the outer must become to keep icing out of the inner.

·       The more clothes one wears inside layer 1, the thicker layer 2 must become to force icing outside of layer 1 and into layer 2 .

·       When the outer layer ices, R2 will decrease and Quilt2 will require airing/deicing or the freezing boundary will creep ever inwards.

 

Corrections on errors and oversights are surely welcome.

[Jerry Adams]

I sort of followed you :)

My 10 degree F temperature was just a guess.  At what temperature did you experience ice buildup on the grand canyon rim?

I see what you’re saying about mass transfer.  The same is true for WPB jackets – you need either a temperature or humidity gradient in order for it to work

In my experience, my quilt is always able to flow out all water vapor my body generates.  Even when I wear damp socks – they’re dry in the morning.  My bag has never got wet (except for rain)

Yeah, it’s complicated about our body being a cylinder.  I pretty much just ignore that.  If my circumference is 40 inches.  Maybe the loft is 3 inches.  Then the circumference of outside the insulation is 2 * pi * 3 inches = 12 inches (assume pi = 3) larger, so the circumference would be 52 inches.  For calculating heat loss just use half way in between – 46 inches.  So it’s 46/40 bigger = 15%.  Maybe bigger than one should ignore.

But, ill do relative, so, for example, if a quilt is good down to 32 F, that would be 60 F temperature difference assuming my skin temp is 92 F.  If I want to go 10F colder then I need 1/6 more insulation.

For icing, just assume a linear drop in temp across the quilt.  Normally, all water vapor will flow through without problem.  But, if at any point in the quilt the temp goes below freezing, at that point the water vapor will freeze and quit flowing through the quilt.  This is more from reading Stephenson than personal experience.  Some Nordic club in NE U.S. has some good documentation about this.

Another factor is there is usually a skin of air next to the outside of the quilt.  There can be a 10F temperature difference across this skin of air.  If the air temp was 22F, then the outside surface of the quilt would be above freezing so no problem.

Yeah, if you’re cowboy camping without tent it makes things worse. Regardless of any skin of air, the quilt surface will be much colder from radiative heat loss.

I sometimes enjoy having the outside of my quilt frosty.  Yet I’m warm inside. Probably something wrong with me to enjoy this :)

[Alan W]

Thanks, Jerry; and apologies for misspelling your name last time.

Overnight lows in Feb 22 on North Rim were high teens for me; but I don’t know the surface temperature on the outside of MLD bivy sack or on outside of quilt.  (your point)

Related, and reconsidering my selecting 92°F as an example of surface temperature in prior note, I would not want to sleep in air that hot.  That’s too hot of a inner surface value for any model of the quilt kit.

Maybe the air inside a comfy winter sleeping kit is more on the order of 75 or 80°F.  (Does anyone know a measured, apt range?)

Alas, a cooler inner surface on Quilt1 shifts the needed ratio of R values to a thicker outer quilt if the selection bogey is kept at 32°F at the interfacial boundary.

[Alan W]

A larger point is that I wonder whether the problem with loss of loft begins with icing during subfreezing ambient temperatures.

Rather than running INTO the freezing point of water, I suspect that the initial wetting and loft problem is running OUT OF the maximum vapor pressure of water when the local temperature inside the quilt begins to approach 32°F, even before reaching 32°F.

I accept that icing is a reality.  However, I expect that ice usually forms from condensed water, excepting maybe in severely sub-0 conditions which few of us encounter.

This is because there is NOT a significant discontinuity in water vapor pressure at the deposition (icing, frost) temperature of 32°F.  (chart following)

[Alan W]

[Alan W]

It’s a water vapor traffic jam, as it were.

o   The saturation concentration of water vapor is declining at a rapid and accelerating rate when ambient temperature drops.

o   Just above freezing the maximum concentration of water in air is literally down to 1/6th of the saturation concentration at 80°F and 1/10th of its maximum at 100°F.

o   It’s as if the water vapor traffic moving outwards starts movement in a saturated 10 lanes on our skin, narrows to 6 lanes, narrows to 5 lanes, 4 lanes, 3 lanes, etc. in rapid succession.

o   — Until there is perhaps a condensation “wreck” (depending on how much vapor is being pushed outwards), followed by icing as colder temperatures creep inwards.

 

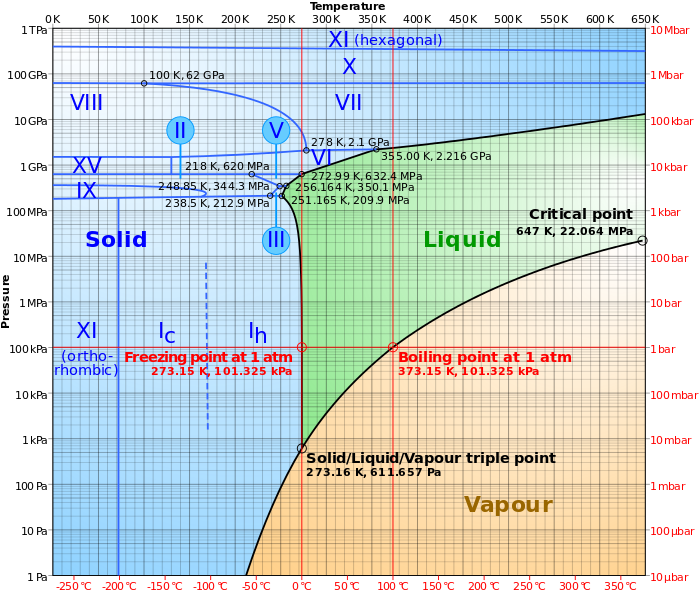
In the chart above, observe that the vapor boundary curve is smooth and continuous at 32°F.

(For those who recognize the chart is for 1 component only (water), reflect that the phase boundary line for ice is vertical from 1 atm down to ambient freezing vapor pressure.  That is, the presence or absence of air, does not measurably affect the freezing point of water below 1 atm system pressure.)

Observe that when local temperatures drop << 50°F in outer layers, we are running OUT OF water vapor pressure, and it is water vapor pressure gradient that drives mass transfer through the quilt kit.

— Or through clothes.  This is the same issue that inevitably plagues our “breathable” rain clothes when ambient temperature falls.

What does it matter?

Maybe the bogey for interfacial temperature for outer synthetic quilt might more aptly be 35 or 40°F to force the initial condensation into the outer layer, as well as placing the frost there.

[Alan W]

Here is another theoretical aspect of diffusive mass transfer model for water vapor that has practical and intuitive application.

It is important that time constant (rate) of vapor diffusion varies inversely with the square of thickness in a planar system, and there are 2 subparts.

o   If the outer layer is ½ as thick as the inner quilt, for example, the outer will tend to dry 4 times as fast, all other things equal.  Of course, they never are, especially comparing down with synthetic.

o   If the outer quilt can be hung flat to dry from two sides, rather than just from 1 surface, it will tend to dry 4 times as fast, all other things equal.  Of course, they never are equal with respect to sunshine and wind.

Still, a thinner and 2-sided outer quilt will tend to dry/de-ice faster than a thicker mummy bag, and this benefit applies even when ambient temperature is < 32°F, —- unless ambient humidity is 100%.

[Alan W]

Which brings another point:  It matters how much water vapor flux is being pushed outbound by our body heat and what the outside humidity is, as well as outside temperature.

o   Yes, I have dried wet clothes inside my sleeping kit many times.

o   However, both more wet clothes inside the quilt system and also colder outside temperature force the “traffic jam” of water vapor to move inwards, forcing condensation in the quilt inwards to occur at somewhat warmer temperatures.

And, it matters what the external ambient humidity is.  Just as a greater ambient humidity increases condensation inside a tent, a greater ambient humidity (freezing fog vs. dry arctic air) increases the condensation and icing inside the quilt because less water vapor can leave the quilt.

[Jerry Adams]

Mammut made a pretty good document about this, then took it off their website, but you can find copies, for example:

The 92F skin temperature is just what they measure for a person sleeping in a sleeping bag.  I would not be comfortable at that air temp, but if I was sleeping at 82F, there’s that air layer next to your skin which has maybe 10F temperature difference, so it would be 92F on my skin.  I think I’d be comfortable sleeping with nothing if the air temp was 82F.

That makes sense that the capacity to carry vapor goes down as the temp drops, like going from 6 lanes down to 1 lane.

Regardless of capacity to carry vapor or how much water vapor is being transported, if the temp goes below freezing at some point, the vapor will form ice crystals at that point.

If a layer is 1/2 as thick it will dry 4 times faster – interesting observation.  That would be another reason to have a synthetic top layer…

I wonder how fast a layer would dry if it was below freezing.  Water does go directly from frozen to gas.  But the rate must be much less than if you melt the ice first.  I wonder if drying is insignificantly small.

Cool diagram of phases of water.  Fortunately, we pretty much stick to the 1 bar line which is less complicated : )

[Author]

Posts